正交多项式

摘要

总结一下可能会遇到的正交多项式

正交多项式定义

一个多项式序列${ {pn}(x)} {n = 0}^\infty$，阶数为$[p_n(x)] = n$,对于每一个$n$，这个多项式序列在开区间$(a,b)$上关于权函数$w(x)$正交，如果：

$$\int_a^bw(x)p_m(x)p_n(x)dx = h_n\delta_{mn}$$

$\delta$为狄克拉函数，且$h_n$为常数
权函数$w(x)$在区间$(a,b)$是连续且正的,下式存在:

$$\mu_n = \int_a^bw(x)x^ndx,n \in N^+$$

则多项式$f$和多项式$g$的内积定义为：

$$\langle{f,g}\rangle = \int_a^bw(x)f(x)g(x)dx$$

区间$(a,b)称为正交区间，正交区间不一定是有限区间$

e.g 三角函数的正交性

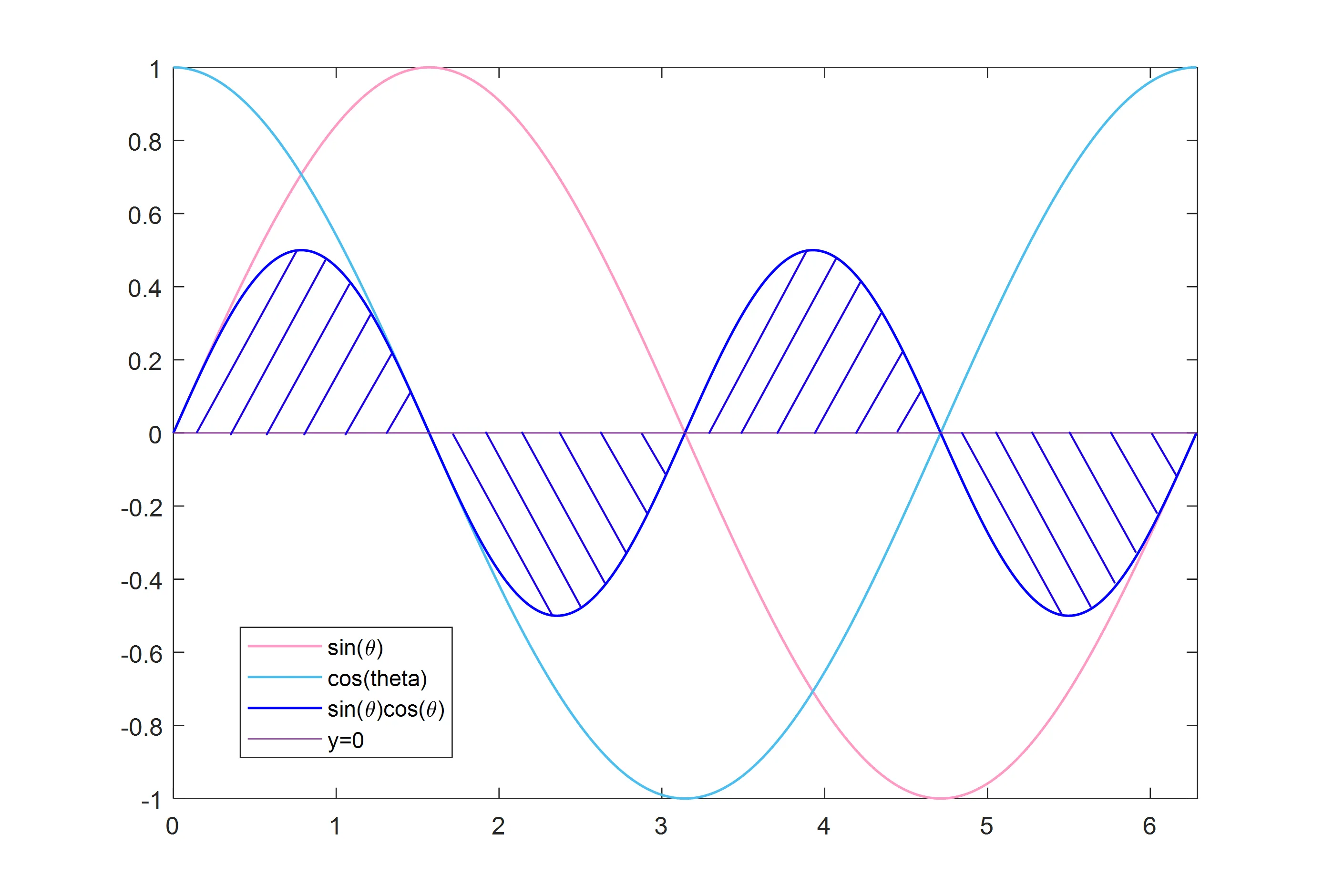
对于三角函数序列$1,sin(\theta),cos(\theta),sin(2\theta),cos(2\theta),…,cos(n\theta)$，$n \in N^+$，他们在区间$(0,2\pi )$的正交性为：

$$\int_0^{2 \pi }sin(n \theta )cos(m \theta) d\theta = \delta_{mn}$$

图中阴影部分的面积加上符号求和为0.

e.g 施密特正交化

施密特正交化方法是将一组线性无关的向量组正交化的方法，对正交化后的向量组进行标准化处理，可进一步得到一组标准正交基。处理步骤如下

$$\begin{array}{l} {\beta _1} = {\alpha _1} \\ {\beta _2} = {\alpha _2} - \frac{ {\left\langle { {\alpha _2},{\beta _1} } \right\rangle } }{ {\left\langle { {\beta _1},{\beta _1} } \right\rangle } }{\beta _1} \\ \cdots \\ {\beta _n} = {\alpha _n} - \frac{ {\left\langle { {\alpha _n},{\beta _1} } \right\rangle } }{ {\left\langle { {\beta _1},{\beta _1} } \right\rangle } }{\beta _1} - \frac{ {\left\langle { {\alpha _n},{\beta _2} } \right\rangle } }{ {\left\langle { {\beta _2},{\beta _2} } \right\rangle } }{\beta _2} - \cdots - \frac{ {\left\langle { {\alpha _n},{\beta _{n - 1} } } \right\rangle } }{ {\left\langle { {\beta _{n - 1} },{\beta _{n - 1} } } \right\rangle } }{\beta _{n - 1} } \\ \end{array}$$

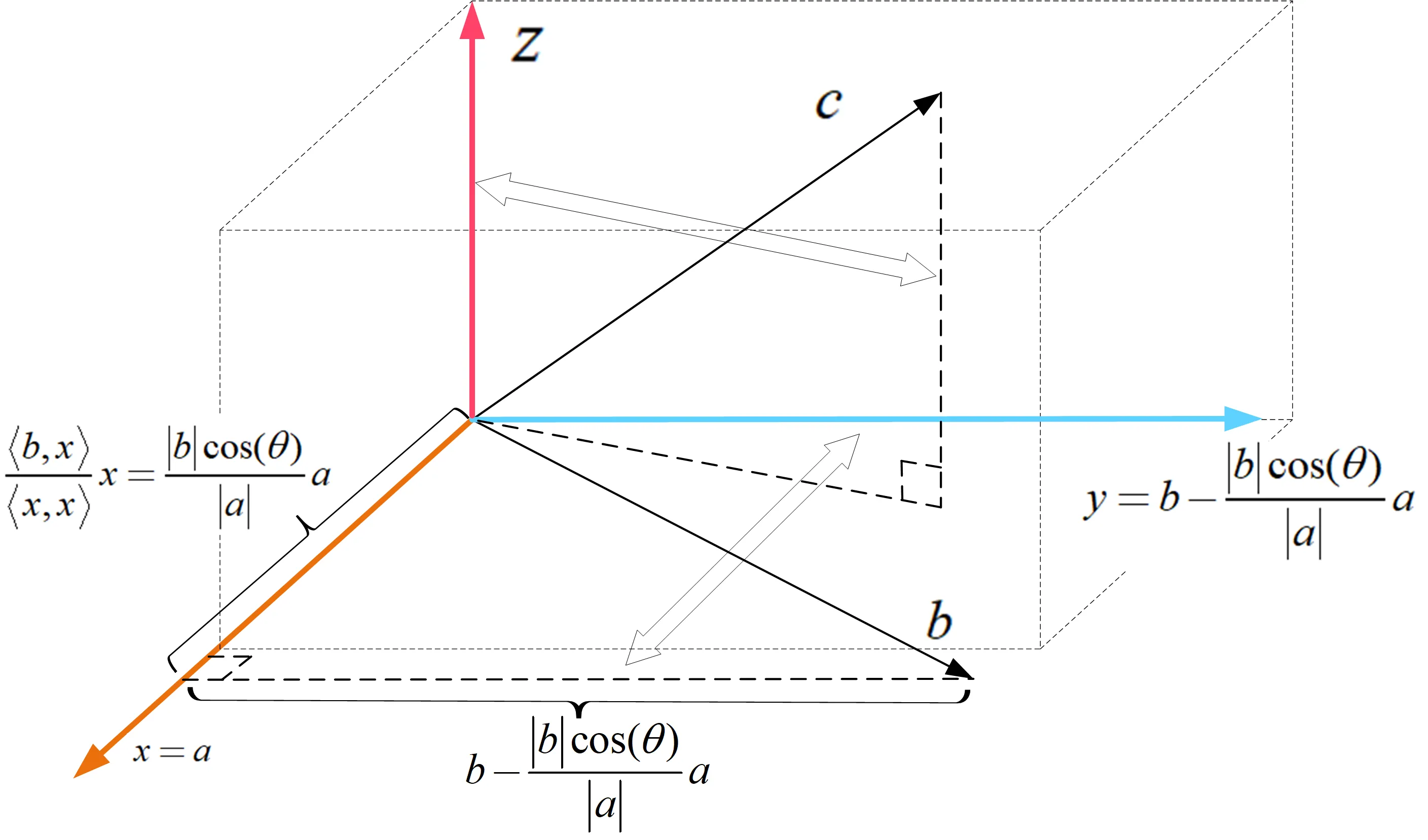
将三维空间中的一组线性无关向量$a,b,c$用施密特正交化方法处理得到正交向量组 $x,y,z$，步骤如下：

$$\begin{array}{l} x = a \\ y = b - \frac{ {\left\langle {b,x} \right\rangle } }{ {\left\langle {x,x} \right\rangle } }x = \frac{ {\left| b \right|\cos (\theta )} }{ {\left| a \right|} }a \\ z = c - \frac{ {\left\langle {c,x} \right\rangle } }{ {\left\langle {x,x} \right\rangle } }x - \frac{ {\left\langle {c,y} \right\rangle } }{ {\left\langle {y,y} \right\rangle } }y \\ \end{array}$$

几何描述如图：

经典正交多项式

如雅克比多项式，切比雪夫多项式，勒让德多项式，拉盖尔多项式，伯恩斯坦多项式，球谐多项式等

雅克比多项式

雅克比多项式是定义在$(-1,1)$上，关于权函数$(1-x)^{\alpha} (1+x)^{\beta} $正交的多项式，其中$\alpha ,\beta > -1$
表达式为：

$$P_n^{ (\alpha,\beta) } (x) = \frac{ \Gamma(\alpha+n+1) }{n!(\alpha+\beta+n+1)} \sum_{m=0}^n \begin{pmatrix} n \\ m \end{pmatrix} \frac{\Gamma(\alpha+\beta+n+m+1)}{\Gamma(\alpha+m+1)}{(\frac{x-1}{2})}^m$$ $$\Gamma(\gamma) = \int_0^{+ \infty } t^{\gamma -1} e^{-t} dt$$

雅克比多项式的正交性：

$$\begin{array}{l} \int_{ - 1}^1 { { {(1 - x)}^\alpha }{ {(1 + x)}^\beta }P_m^{(\alpha ,\beta )}(x)P_n^{(\alpha ,\beta )}(x)dx} \\ = \frac{ { {2^{\alpha + \beta + 1} } } }{ {2n + \alpha + \beta + 1} }\frac{ {\Gamma (\alpha + n + 1)\Gamma (\beta + n + 1)} }{ {n!\Gamma (\alpha + \beta + n + 1)} }{\delta _{mn} } \\ \end{array}$$

勒让德多项式

勒让德多项式是定义在区间 $(−1,1) $上关于权函数1正交的多项式。勒让德多项式实际上是雅克比多项式在 $\alpha=\beta=0$ 时的特殊情况
表达式为：

$$P_n(x) = \frac{1}{2^n n!} \frac{d^n}{dx^n} [ (x^2-1)^n ]$$

递推公式为：

$$(n+1)P_{n+1}(x) = (2n+1)xP_n(x)-nP_{n-1}(x)$$

正交性：

$$\int_{-1}^1 P_m(x)P_n(x)dx = \frac{2}{2n+1}\delta_{mn}$$

前6阶勒让德多项式：

$$P_0(x) = 1$$ $$P_1(x) = x$$ $${P_2}(x) = \frac{3}{2}{x^2} - \frac{1}{2}$$ $${P_3}(x) = \frac{5}{2}{x^3} - \frac{3}{2}x$$ $${P_4}(x) = \frac{ {35} }{8}{x^4} - \frac{ {15} }{4}{x^2} + \frac{3}{8}$$ $${P_5}(x) = \frac{ {63} }{8}{x^5} - \frac{ {35} }{4}{x^3} + \frac{ {15} }{8}x$$ $${P_6}(x) = \frac{ {231} }{ {16} }{x^6} - \frac{ {315} }{ {16} }{x^4} + \frac{ {105} }{ {16} }{x^2} - \frac{5}{ {16} }$$

图像为：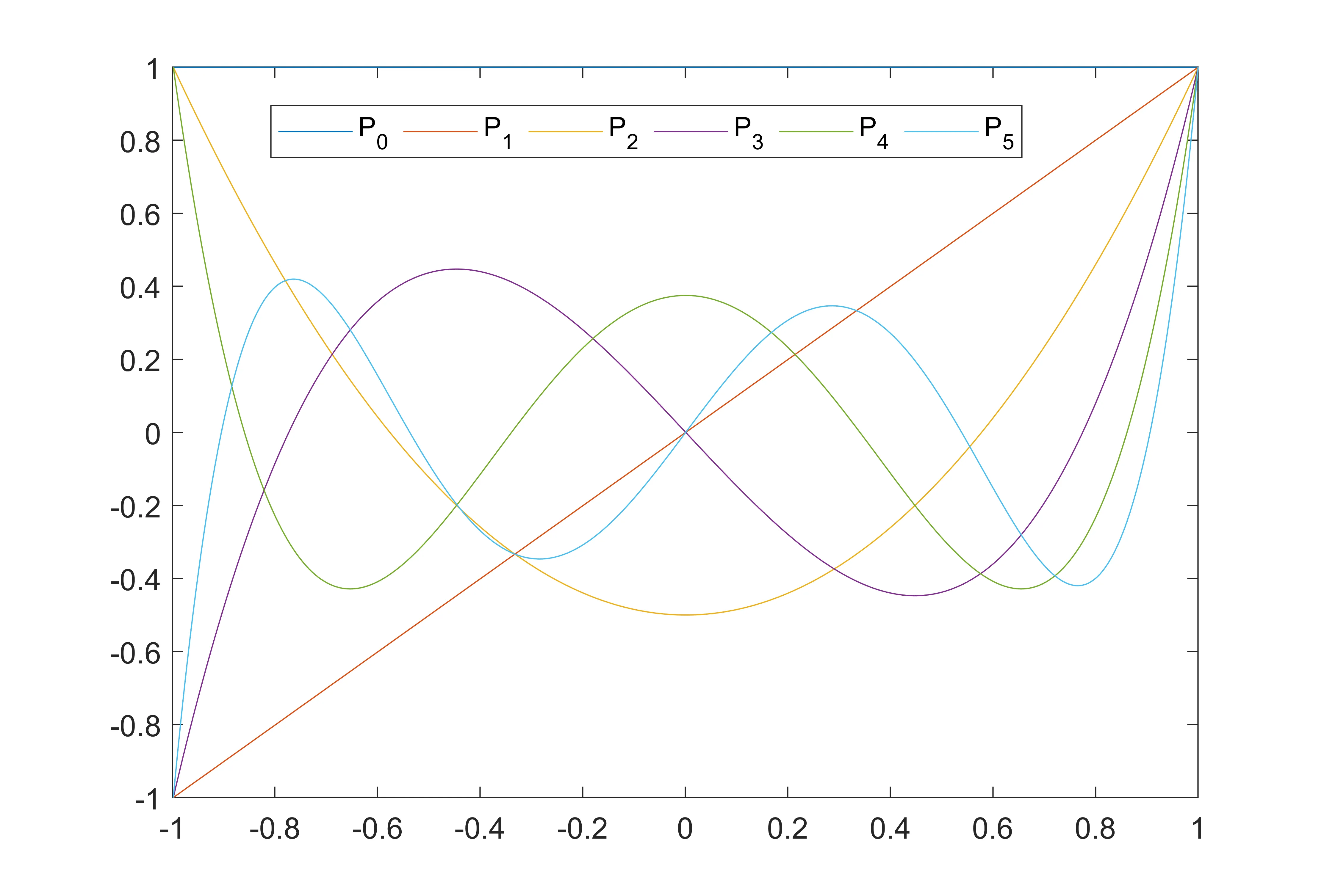

切比雪夫多项式

切比雪夫多项式是定义在区间 $(−1,1)$ 上关于权函数 $\frac{1}{\sqrt{1-x^2} }$ 正交的多项式

第一类切比雪夫多项式

$$T_n(x) = cos(n\theta)$$

令$x = cos(\theta)$，则$T_n(x) = cos(n \arccos(x))$，
第一类切比雪夫多项式正交性：

$$\int_{-1}^1 \frac{1}{\sqrt{1-x^2} } T_m(x) T_n(x)dx = \begin{cases}0 \quad m \neq n \\ \pi \quad n=m=0 \\ \frac{\pi}{2} \quad n=m \neq 0 \end{cases}$$

第一类切比雪夫多项式递推公式：

$${T_{n + 1} }(x) = 2x{T_n}(x) - {T_{n - 1} }(x)$$

第一类切比雪夫多项式的前6项：

$$T_0(x) = 1$$ $$T_1(x) = x$$ $$T_2(x) = 2x^2-1$$ $$T_3(x) = 4x^3-3x$$ $$T_4(x) = 8x^4-8x^2+1$$ $$T_5(x) = 16x^5-20x^3+5x$$ $$T_6(x) = 32x^6-48x^4+18x^2-1$$

第一类切比雪夫多项图像：

第二类切比雪夫多项式

$${T_n}(x) = \frac{ {\sin [(n + 1)\theta ]} } { {\sin \theta } }$$

第二类切比雪夫多项式的正交为：

$$\int_{-1}^1 \sqrt{1-x^2}{T_m}(x){T_n}(x)dx=\begin{cases}0 \quad m\neq n \\ \frac{\pi}{2} \quad m = n \end{cases}$$

第二类切比雪夫多项式的递推公式：

$${T_{n + 1} }(x) = 2x{T_n}(x) - {T_{n - 1} }(x)$$

第二类切比雪夫多项式的前6项：

$$T_0(x) = 1$$ $$T_1(x) = 2x$$ $$T_2(x) = 4x^2-1$$ $$T_3(x) = 8x^3-4x$$ $$T_4(x) = 16x^4-12x^2+1$$ $$T_5(x) = 32x^5-32x^3+6x$$ $$T_6(x) = 64x^6-80x^4+24x^2-1$$

第二类切比雪夫多项图像：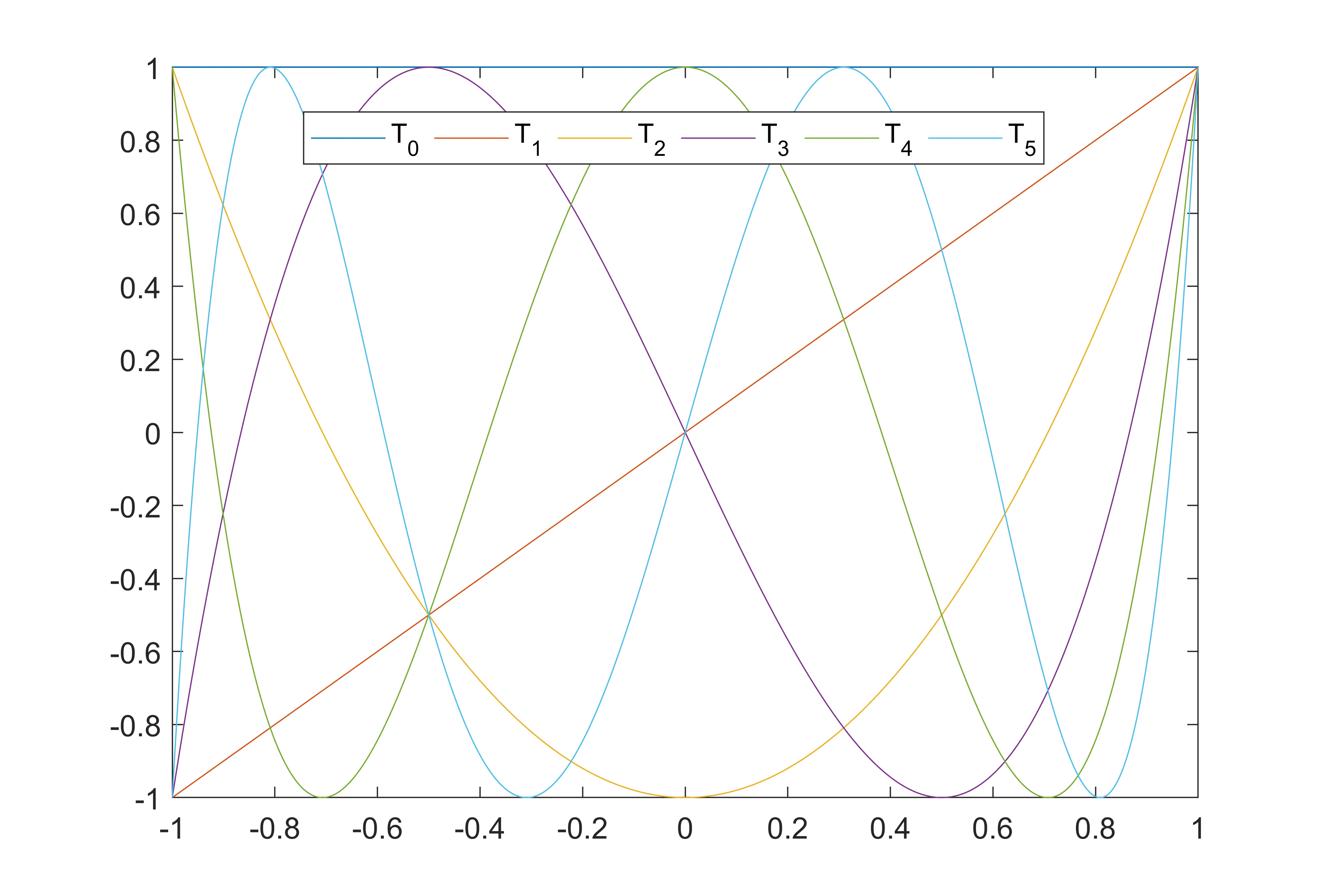

拉盖尔多项式

拉盖尔多项式是定义在区间 $(0,+\infty)$ 上关于权函数 $e^{-x}x^a$ 正交的多项式
拉盖尔多项式的正交关系：

$$\int_0^{ + \infty } { {x^\alpha }{e^{ - x} }L_m^{(\alpha )}(x)L_n^{(\alpha )}(x)dx} = \frac{ {\left( {n + \alpha } \right)!} }{ {n!} }{\delta _{mn} }$$

拉盖尔多项式的递推关系：

$${L_{n + 1} }(x) = \frac{ {(2n + 1 - x){L_n}(x) - n{L_{n - 1} }(x)} }{ {n + 1} }$$

前6项拉盖尔多项式$(\alpha = 0)$：

$$L_0(x) = 1$$ $$L_1(x) = -x+1$$ $$L_2(x) = \frac{1}{2}x^2-2x+1$$ $$L_3(x) = -\frac{1}{6}x^3+\frac{3}{2}x^2-3x+1$$ $$L_4(x) = \frac{1}{24}x^4-\frac{2}{3}x^3+3x^2-4x+1$$ $$L_5(x) = -\frac{1}{120}x^5+\frac{5}{24}x^4-\frac{5}{3}x^3+5x^2-5x+1$$ $$L_6(x) = \frac{1}{720}x^6-\frac{1}{20}x^5+\frac{5}{8}x^4-\frac{10}{3}x^3+\frac{15}{2}x^2-6x+1$$

前6项拉盖尔多项式的图像：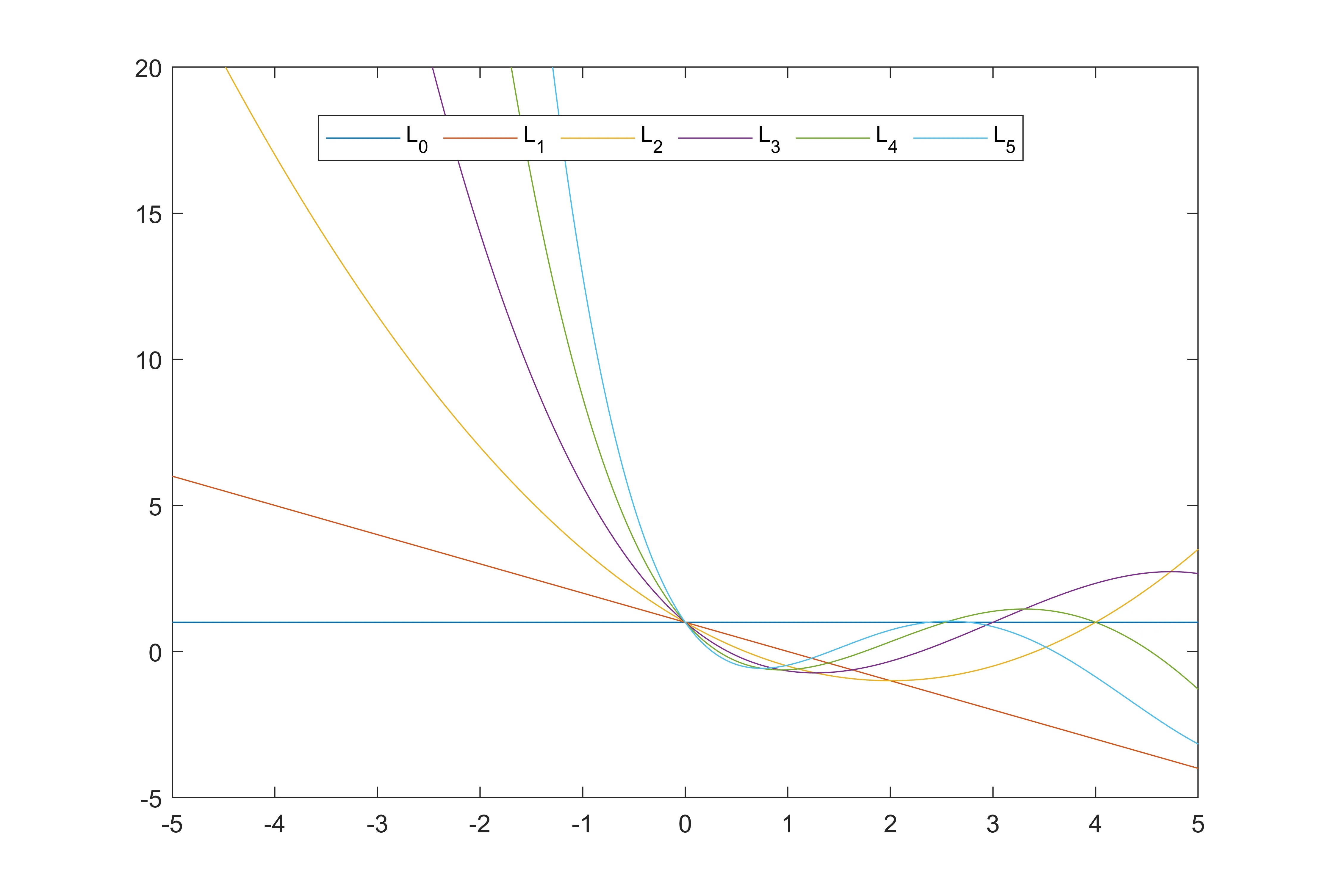

埃尔米特多项式

埃尔米特多项式是定义在区间$(-\infty,+\infty)$上关于权函数$e^{x^2}$正交的多项式
埃尔米特多项式分为概率论中的埃尔米特多项式和物理中的埃尔米特多项式，概率论的埃尔米特多项式是首一多项式（最高次项系数等于1），而物理学的埃尔米特多项式的最高次项系数等于$2n$，这里只介绍物理学中使用的埃尔米特多项式
埃尔米特多项式的表达式为：

$$H_n(x) = (-1)^n e^{x^2} \frac{d^n}{dx^n}e^{-x^2}$$

埃尔米特多项式的正交性：

$$\int_{-\infty}^{+\infty} H_m(x)H_n(x)e^{-x^2}dx = \sqrt{\pi}2^n n! \delta_{mn}$$

埃尔米特多项式的递推公式：

$$H_{n+1}(x) = 2xH_n(x)-2nH_{n-1}(x)$$

前6项埃尔米特多项式为：

$$H_0(x) = 1$$ $$H_1(x) = 2x$$ $$H_2(x) = 4x^2-2$$ $$H_3(x) = $8x^3-12x$$ $$H_4(x) = 16x^4-48x^2+12$$ $$H_5(x) = 32x^5-160x^3+120x$$ $$H_6(x) = 64x^6-480x^4+720x^2-120$$

前6项埃尔米特多项式图像：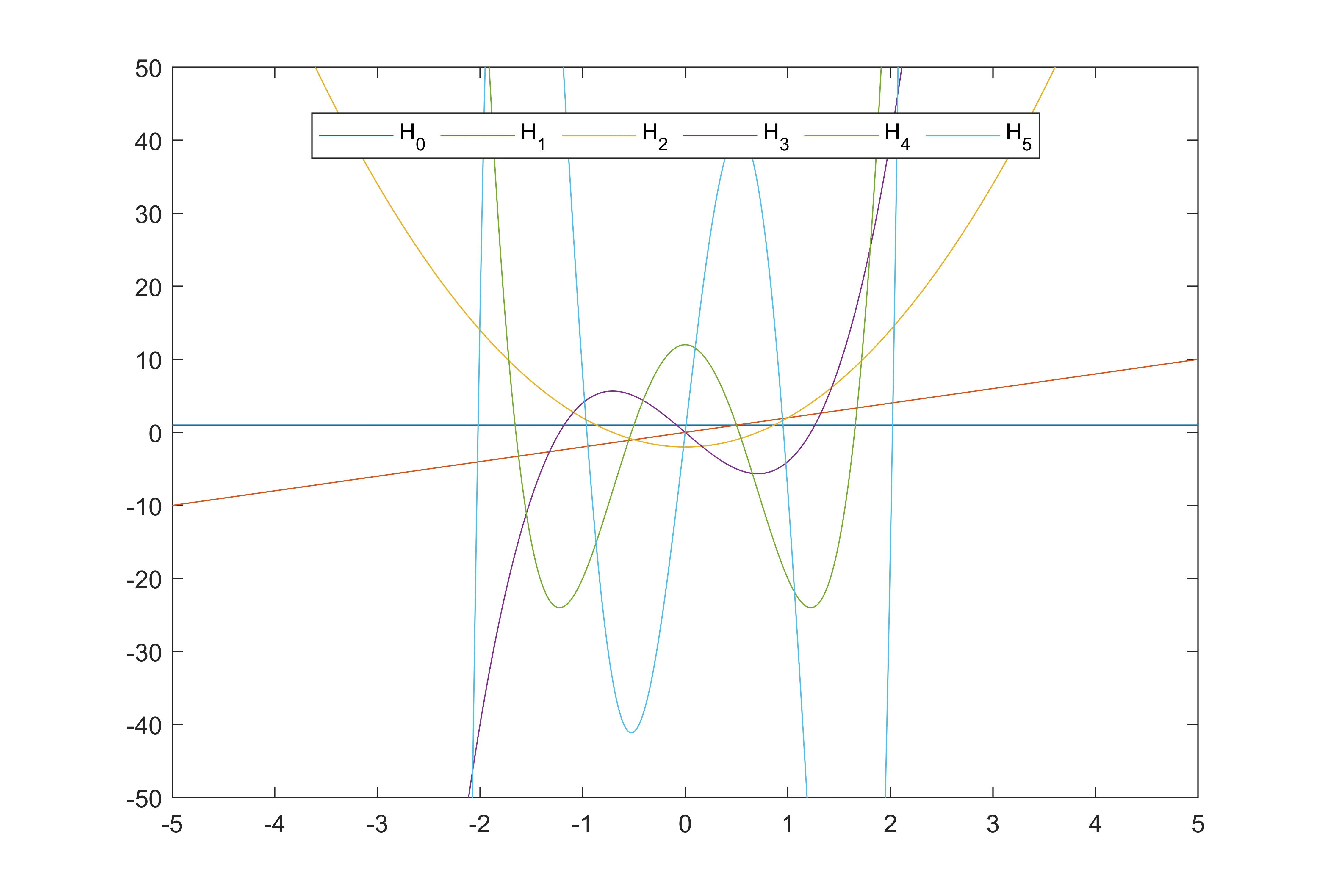

正交多项式的应用

仅以一个小的例子来说明正交多项式在函数拟合中的应用
实验中使用的测试函数为 $y=4x+3x^2+cos(x)+sin(2x)+e^x$，定义区间为 $(−2,2)$ ，实验比较了多项式展开3项时不同多项式的拟合均方误差（MSE），归一化均方误差

输出

MSE_power =
    0.0131
NMSE_power =
    0.0419
MSE_legendre =
    0.0131
NMSE_legendre =
    0.0419
MSE_chebyshev =
    0.0131
NMSE_chebyshev =
    0.0419
MSE_laguerre =
    0.0131
NMSE_laguerre =
    0.0419
MSE_hermite =
    0.0067
NMSE_hermite =
    0.0215

可以看出埃尔米特的拟合误差较小，其他相当

% 正交多项式测试
clear
clc
% 采样点数
N = 1000 ; 
% 正交多项式阶数
M = 3 ;   
% 拟合函数区间为（-2,2）
x = linspace(-2,2,N)' ; 
% 生成被拟合的函数，包括指数函数，余弦函数，幂函数成分
y =  4*x + 3*x.^2 + cos(x) + exp(x) + sin(2*x);
 
% 生成幂级数组成的基矩阵
P1 = power_p(x,M) ;
% 生成勒让德多项式组成的基矩阵
P2 = legendre_p(N,M) ;
% 生成切比雪夫多项式组成的基矩阵
P3 = chebyshev_p(N,M) ;
% 生成拉盖尔多项式组成的基矩阵
P4 = laguerre_p(N,M) ;
% 生成诶尔米特多项式组成的基矩阵
P5 = hermite_p(N,M) ;
 
%% 用最小二乘拟合y
% c1对应幂级数系数
c1 = P1\y ;
% c2对应勒让德系数
c2 = P2\y ;
% c3对应切比雪夫系数
c3 = P3\y ;
% c4对应拉盖尔系数
c4 = P4\y ;
% c5对应埃尔米特系数
c5 = P5\y ;
 
%% 求MSE和NMSE
MSE_power = norm(y-P1*c1)/N 
NMSE_power = norm(y-P1*c1)/norm(y) 
 
MSE_legendre = norm(y-P2*c2)/N 
NMSE_legendre = norm(y-P2*c2)/norm(y) 
 
MSE_chebyshev = norm(y-P3*c3)/N 
NMSE_chebyshev = norm(y-P3*c3)/norm(y) 
 
MSE_laguerre = norm(y-P4*c4)/N 
NMSE_laguerre = norm(y-P4*c4)/norm(y) 
 
MSE_hermite = norm(y-P5*c5)/N 
NMSE_hermite = norm(y-P5*c5)/norm(y) 
 
figure(1)
plot(x,y,'r-',x,P1*c1,'b-',x,P2*c2,'k-',x,P3*c3,'y-',x,P4*c4,'g-',x,P5*c5,'m-')
legend('original','power','legendre','chebyshev','laguerre','hermite')
 
function [P] = power_p(x,M)
 
for m = 1:M
    P(:,m) = x.^(m-1) ;
end
end
 
function [P] = legendre_p(N,NN)
% 本函数生成N*M的勒让德基矩阵
s = linspace(-1,1,N)' ;
P = zeros(N,NN) ;
P(:,1) = ones(N,1) ;
P(:,2) = s ;
for n = 3 : NN
    P(:,n) = ((2 * n - 3) * s .* P(:,n - 1) - (n - 2) * P(:,n - 2)) / ( n -1 ) ;
end
end
 
function [P] = chebyshev_p(N,M)
% 本函数生成N*M的切比雪夫基矩阵
x = linspace(-1,1,N)' ;
P = zeros(N,M) ;
P(:,1) = ones(N,1) ;
P(:,2) = x ;
for k = 3:M
    P(:,k) = 2*x.*P(:,k-1) - P(:,k-2) ;
end
end
 
function [P] = laguerre_p(N,M)
% 本函数生成N*M的拉盖尔基矩阵
x  = linspace(-2,2,N)' ;
P = zeros(N,M) ;
P(:,1) = ones(N,1) ;
P(:,2) = -x + ones(N,1) ;
for m = 3:M
    P(:,m) = ((2*(m-2)+1-x).*P(:,m-1)-(m-2)*P(:,m-2))./(m-1) ;
end
end
 
function [P] = hermite_p(N,M) 
% 本函数生成N*M的埃尔米特基矩阵
x = linspace(-2,2,N)' ;
P = zeros(N,M) ;
P(:,1) = ones(N,1) ;
P(:,2) = 2*x ;
 
for m = 2:M
    P(:,m+1) = 2*x.*P(:,m-) - 2*(m-1)*P(:,m-1) ;
end
end