多目标优化笔记

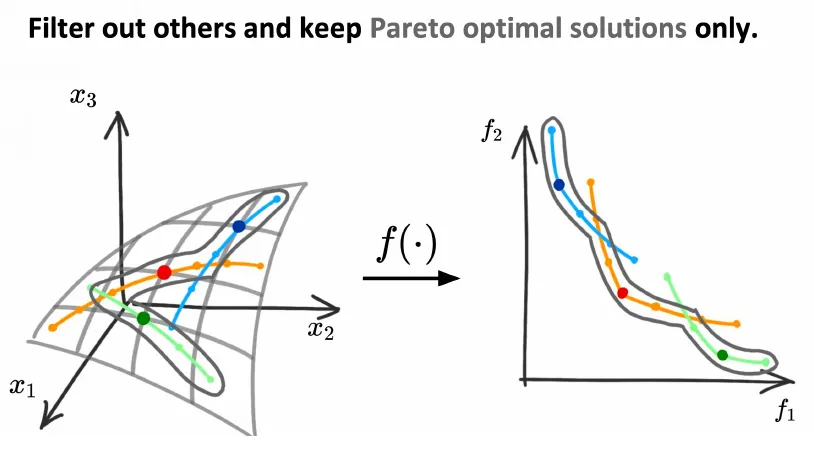
摘要

多目标优化 ( MOO ) - Multi-Objective Optimization

从问题定义，单目标、多目标，无约束、有约束方面了解多目标优化

基础

无约束的单目标优化问题

$$\min_{x} f(x),x \in R^{N}$$

无约束的多目标优化问题

$$\min_{x} F(x) = [f_1(x), f_2(x),\cdots, f_n(x)], x \in R^{N}$$

$ n $ 为子目标的数量，$ f_n(x) $为一阶可导目标函数 $F(x)$ 的子函数

有约束的单目标优化问题

$$\begin{array}{lcl} \min_{x} & f(x) & \\ \text { s.t. } & g_{i}(x) \geq 0 & , i \in[1, M] \\ & h_{j}(x)=0 & , j \in[1, L] \end{array}$$

$\text { s.t. }$ 为 subject to ，受限于的缩写，设 $ D $ 为可行域

$$D = \{x | g_i(x) \geq 0, i \in [1, M], h_j(x) =0 , j \in [1,L] \}$$

有约束的多目标优化问题

$$\begin{array}{lcl} \min_x & F(x) = [f_1(x), f_2(x),\cdots, f_n(x)]\\ \text{s.t.} & g_i(x) \geq 0 ,\quad i\in(1, M) \\ & h_j(x) = 0 ,\quad j \in (1,L) \end{array}$$

设 $ D $ 为可行域

$$D = \{x | g_i(x) \geq 0, i \in [1, M], h_j(x) =0 , j \in [1,L] \}$$

MOO 的解集

对于 MOO，通常没有解 $ x^\ast \in D $, 使 $ f_i(x), \forall i \in [1,N] $ 同时处于最优解，因此单目标优化问题的解在 MOO 中通常不适用

MOO 中的解集分为 绝对有效解，有效解，弱有效解

设 $R^N $为 $N$ 维的实向量空间，$y=(y_1,y_2,\cdots, y_N)^{T}$，$z=(z_1,z_2,\cdots, z_N)^{T}$

$$\begin{cases}\text { 相等 } & y=z \Leftrightarrow y_{i}=z_{i}, i=1,2, \ldots, N \\ \text { 严格小于 } & y<z \Leftrightarrow y_{i}<z_{i}, i=1,2, \ldots, N \\ \text { 小于 } & y \leqq z \Leftrightarrow y_{i} \leqslant z_{i}, i=1,2, \ldots, N \\ \text { 小于且不相等(支配) } & y \leqslant z \Leftrightarrow y_{i} \leqslant z_{i}, i=1,2, \ldots, N, y \neq z\end{cases}$$

Pareto 支配（Pareto Dominance）

$ \forall x_1, x_2 \in R^{N} $， 对于 $ k = 1,\cdots,K $，都有 $ f_k(x_1) \leqslant f_k(x_2)$，则 $ x_1 $ 支配 $ x_2 $

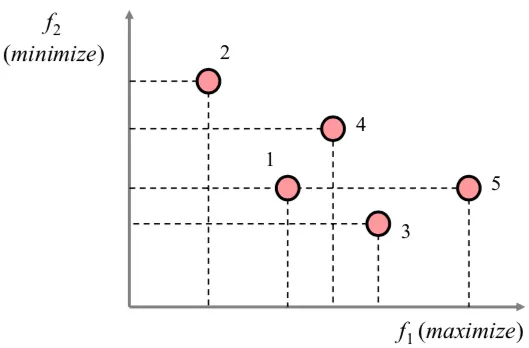
Pareto 解集（绝对最优解）

$ x^{\ast}{\in}{D} $ ， $ \forall x \in D,\quad f(x^\ast) {\leqq} f(x) $ ，即 $ \forall k \in 1,\cdots,K, \quad fK(x^\ast) \leqq f{K}(x) $ ，则 $ x^\ast $ 为 MOO 问题的最优解

Pareto 解集（有效解）

$x^\ast\in{D}$ ，若 $f_k(x)\leq f_k(x^\ast) \wedge \exists i,f_i(x) < f_i(x^\ast),i\in [1,k]$ 不成立，则 $x^\ast$ 是 MOO 问题的有效解，也叫 Pareto 最优解，其含义是如果 $x^\ast$ 是 Pareto 最优解，则找不到这样的可行解 $x\in{D}$ ，使得 $f(x)$ 的每个目标值都不比 $f(x^\ast)$ 的目标值坏,并且 $ f (x) $ 至少有一个目标比 $f(x^\ast)$ 的相应目标值好，即 $ x^\ast $ 是最好的，不能再进行改进（Pareto 改进）

Pareto 解集（弱有效解）

$x^\ast\in{D}$ ，如果不存在 $x\in{D}$，使得 $f(x)<f(x^\ast)$ ，即

$$f_k(x) < f_k(x^*) \quad \wedge \quad \forall k \in [1,K]$$

则 $x^\ast$ 是 MOO 问题的有效解，其含义是如果 $x^\ast$ 是弱有效解,则找不到这样的可行解 $x\in{D}$，使得 $f(x)$ 的每个目标值都比 $f(x^\ast)$ 的目标值严格（ $<$ ）的好

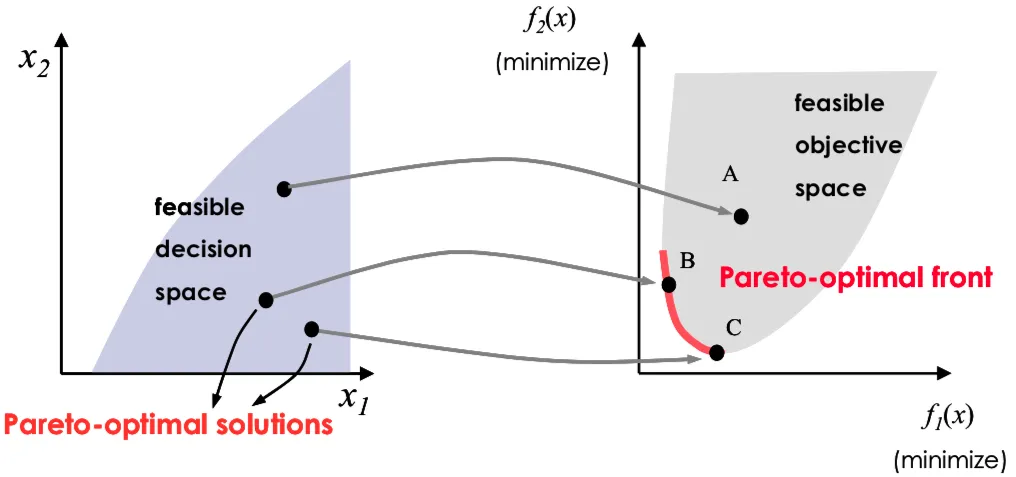
Pareto 最优解集（Pareto-optimal Set）

给定问题的有效解集（Pareto 最优解）构成的解集，集合中的解是相互非支配的，两两非支配关系，简称 $PS$

Pareto 最优前沿（Pareto-optimal Front）

Pareto 每一个解对应的目标值向量组成的集合，简称 $PF$

$$PF = \{F(x)|x\in PS\}$$

MOO 的最优性条件

约束规格定义：对优化问题的约束函数，附加某些限制条件，使得其最优解满足的最优性条件

下面给出一个严格条件下多目标优化的充分必要条件，给出的充要条件前，先引入了约束规格条件

$$\begin{aligned} \min _{x \in \hat{D}} F(x) &=\sum_{k=1}^{K} f_{k}(x) \\ \hat{D} &=x \in D \mid f(x) \leq f(\hat{x}) \end{aligned}$$

定理：设 $ f (x)$ ，$ g(x) $ 为凸函数,且在 $x \in D$ 处可微，$h(x)$ 为线性函数，且 $\hat{D} = x \in D|f (x) \leq f (\hat{x})$ 满足 $ KKT $ 约束规格，则 $x^\ast$ 是 MOO 的有效解的充分必要条件是存在 $ \lambda \in R^K , u \in R^M , v \in R^L$， 使得

$$\left\{\begin{array}{l} \nabla_{x} L\left(x^{*}, \lambda^{*}, u^{*}, v^{*}\right)=\nabla f\left(x^{*}\right) \lambda^{*}+\nabla g\left(x^{*}\right) u^{*}+\nabla h\left(x^{*}\right) v^{*}=0 \\ u^{* T} g\left(x^{*}\right)=0 \\ \lambda^{*}>0, u^{*} \geq 0 \end{array}\right.$$

MOO 的经典算法

线性加权法

根据 $f(x)$ 的重要程度，设定权重进行线性加权

$$\begin{array}{r} & \min _{x} \sum_{k=1}^{K} \lambda_{k} f_{k}(x) \\ \text { s.t. } & g_{i}(x) \geq 0,\quad i \in[1, M] \\ & h_{j}(x)=0,\quad j \in[1, L] \end{array}$$

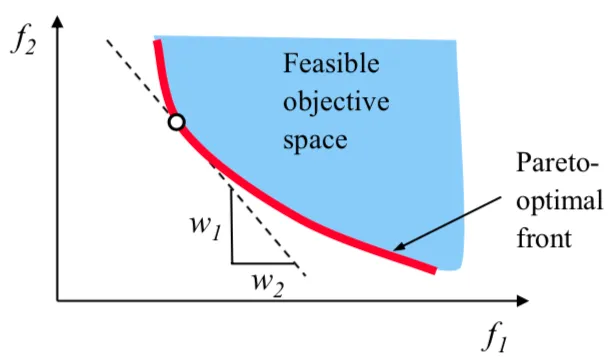
于是就变成了单目标优化问题，上述问题存在有效解的条件，对于给定的 $\lambda \in \Lambda^{++}$ ，则上述问题的最优解是 MOO 问题的有效解，其中

$$\Lambda^{++}=\left\{\lambda \mid \lambda_{k}>0, k=1,2 \ldots K, \sum_{k=1}^{K} \lambda_{k}=1\right\}$$

• 优点：实现简单，有成熟的算法求解
• 缺点：$\lambda_k$ 难以确定，求出的解的优劣无法确定

主要目标法

也称 $\epsilon$-约束方法

$$\begin{array}{l} & \min _{x} & f_{p}(x) \\ \text { s.t. } & f_{k}(x) &\leq \epsilon_{k} &,k=1, \ldots, K, k \neq p \\ & g_{i}(x) &\geq 0, i \in[1, M] \\ & h_{j}(x) &= 0, j \in[1, L] \end{array}$$

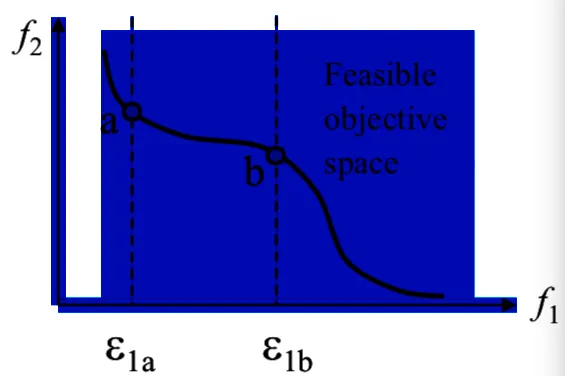
$\epsilon$-约束方法从 $K$ 个目标中选择最重要的子目标作为优化目标,其余的子目标作为约束条件。每个子目标,通过上界 $\epsilon_{K}$ 来约束

主要目标法最优解和 MOO 解集的关系

• 主要目标法最优解是 MOO 解的弱有效解

• 若主要目标 $f_p (x)$ 是严格凸函数，可行域为 $\hat{D}$ 的凸集，则主要目标法最优解是 MOO 解的有效解

界限值 $\epsilon$ 的选取

可以取子目标函数的上限值

$$\min \left\{f_{k} \mid f_{k}(x), k=1, \ldots, K, k \neq p\right\} \leq \epsilon_{k}$$

这种取法可以使得某些 $f_k(x)$ 留在可行域 $\hat{D}$ 内,并且 $\hat{D}$ 内有较多的点靠近 $f_k (x)$ 的最优解

• 优点：简单，能应用到凸函数和非凸函数场景下
• 缺点：$\epsilon_k$ 如果取值不合适，可行域 $\hat{D}$ 可能为空值

逼近目标法

提出一个目标值 $f^0 = (f_1^0,f_2^0,\cdots,f_k^0)$，使得每个目标函数 $f_k(x)$ 都逼近对应的目标值

$$\begin{array}{l} L = (f(x), f^0) & = ||f(x) - f^0 ||^{\lambda}_{2} \\ &= \sum_{k=1}^{K} \lambda_k(f_k(x)-f^0)^2,\lambda \in \Lambda^{++} \end{array}$$

和机器学习中的损失函数类似，是一个单目标优化问题，可以通过经典的方法进行求解，这里求解的最优解和有效解及弱有效解没有直接的联系，反映了决策者希望的目标值

梯度下降算法

这是一种直接优化的方法，而上面提到的算法都是采取先验的知识将多目标优化转化成单目标优化

最速梯度下降

简单起见，将讨论问题限制在无约束的单目标优化问题，并要求无约束的单目标优化问题中的 $f (x)$ 具有一阶连续偏导数，对于这类问题，能够从某一点出发，选择目标函数 $f (x) $ 下降最快的方向进行搜索，尽快达到最小值，问题是如何选择下降最快的方向

$$DF(x;d) = \nabla f(x)^T d$$

求 $f(x)$ 在点 $x$ 处的下降最快的方向导数，归结为求如下最优化问题

$$\min \nabla f(x)^T d \\ \text{s.t.} \quad ||d|| \leq 1$$

其中 $||\cdot||$ 为欧式距离，上述问题的解为

$$d = -\frac{\nabla f(x)}{||\nabla f(x)||}$$

负梯度方向为最速下降方向，最速下降法的迭代公式为

$$x^{t+1} = x^t + \lambda_k d^{(k)}$$

其中，$\lambda _k$ 可以通过一维搜索来得到

多目标梯度下降算法

设当前为 $t+1$ 轮迭代，梯度迭代公式

$$x^{t+1} = x^t + \lambda \cdot d^{t}$$

多目标优化的方向导数

$$\nabla f_k(x)^T d,k = 1,2,\cdots,K$$

定义最大方向导数

$$M_x(d^t) = max\{ \nabla f_k(x)^T d^t \mid k = 1,2,\cdots,K\}$$

多目标问题的最速梯度下降方向，可以归结为求解以下问题

$$\begin{array}{l} \min & M_x(d^t) + \frac{1}{2} \| d^t \| ^2 \\ \text{s.t.} & d^t \in R \end{array}$$

上述优化问题是闭且强凸优化问题，一定存在最优解，令 $M_x (d^t) = \alpha$，可以将一阶偏导项消去

$$\begin{array}{l} \min & \alpha + \frac{1}{2} \|d^t \|^2 \\ \text{s.t.} & \nabla f_k(x)^T d^t \leq \alpha ,k = 1,2,\cdots,K \\ & d^t \in R \end{array}$$

上述问题为带线性不等式约束的凸二次规划问题

令 $d^\ast$，$a^\ast$ 为上述优化问题的最优解，得到

• 若 $x^\ast$ 为 Pareto 最优，则 $d^\ast=0,a^\ast=0$
• 若 $x^\ast$ 不为 Pareto 最优，则 $a^\ast<0$

且

$$\alpha \leq-\frac{1}{2} \|\left. d^{t}\right|^{2}<0 \\ \nabla f_{k}(x)^{T} d^{t} \leq \alpha, k=1, \cdots, K$$

因此

• 如果 $d^\ast = 0$，则说明此时不存在下降方向,使得所有的目标都下降
• 如果 $d^\ast \neq 0$，则有 $\nabla f_{k}(x)^{T} d^{t} < 0$，则 $d^t$ 是一个有效的多目标搜索方向，按如下公式更新，即可以使目标函数下降

$$\begin{array}{l} x^{(t+1)}&=& x^{t}+\lambda \cdot d^{t} \\ f_{k}\left(x^{(t+1)}\right) &\leq& f_{k}\left(x^{t}\right), k=1, \ldots, K \end{array}$$

多任务学习（MTL）

多任务学习（MTL）- Multi-Task Learning

定义

在同一时间学习多个任务，求得最优解

设有 $N$ 个样本点 ${ x,y_i^1,y_i^2,\cdots, y_i^T},i \in N$，其中 $T$ 为任务数量，$y_i^t$ 是第 $t^{th}$ 个任务，第 $i^{th}$ 个样本点标签，定义为

$$f^t(x;\theta^{sh},\theta^t):X \rightarrow Y^t$$

其中 $\theta^{sh}$ 为多个任务的共享参数，$\theta^t$ 为单个任务的独有参数

$Loss$ 为

$$L^t(\_,\_) = Y^t \times Y^t \rightarrow R^+$$ $$\min_{\theta^{sh} ,\theta} = \sum_{t=1}^{T} c^t \hat{L}^{t}(\theta^{sh},\theta)$$

$c^t$ 为每个具体任务的权重，每个具体任务 $t$ 的 $Loss$ 为

$$\hat{L}^t(\theta^{sh},\theta) \triangleq \frac{1}{N} \sum_t L(f^t(x;\theta^{sh}, \theta^t), y^t_i)$$

多任务学习转化为多目标优化

将多任务学习转换为 MOO 问题求解，定义

$$\min _{\theta^{s h}, \theta} L\left(\theta^{s h}, \theta^{1}, \ldots, \theta^{T}\right)=\min _{\theta^{s h}, \theta}\left(\hat{L}^{1}\left(\theta^{s h}, \theta^{1}\right), \cdots, \hat{L}^{T}\left(\theta^{s h}, \theta^{T}\right)\right)$$

多目标优化的目的是求得 Pareto 最优解，多目标优化的 Pareto 最优解定义

一个解 $\theta$ 支配另一个解 $\bar{\theta}$ ，如果

$$\hat{L}(\theta^{sh},\theta^t) \leq \hat{L}(\bar{\theta}^{sh},\bar{\theta}^t)$$

对于所有的任务 $t$ 都成立，且

$$L(\theta^{sh},\theta^1,\theta^2,\cdots,\theta^{T}) \neq L(\bar{\theta}^{sh},\bar{\theta}^1,\bar{\theta}^2,\cdots, \bar{\theta}^T)$$

一个解 $\theta^{\ast}$ 称为 Pareto 最优解的集合称为 Pareto 最优解集，其图像称为 Pareto 前沿（Pareto Front）

多任务求解：单个 Pareto 解

问题转化

单个 Pareto 解使用了多重梯度下降法，由多目标优化的 $KKT$ 条件，得

存在 $\alpha^1,\alpha^2,\cdots,\alpha^T \geq 0$，使得

$$\begin{array}{r} \sum_{t=1}^{T} \alpha^T = 1 \\ \sum_{t=1}^{T} \alpha^t \nabla_{\theta^{sh}} \hat{L}(\theta^{sh},\theta^{t}) = 0 \end{array}$$

对应所有的任务 $t$

$$\nabla_{\theta^t}\hat{L}(\theta^{sh},\theta^t) = 0$$

满足上式的解称为 Pareto 平衡点（Pareto Stationary Point），Pareto 最优点都是 Pareto 平稳点，反之不一定成立，考虑如下的优化问题

$$\begin{gathered} \min _{\alpha^{1}, \cdots ,\alpha^{T}}\left\|\sum_{t=1}^{T} \alpha^{t} \nabla_{\theta s h} \hat{L}^{t}\left(\theta^{s h}, \theta^{t}\right)\right\| \\ \sum_{t=1}^{T} \alpha^{t}=1, \alpha^{t} \geq 0, \forall t \end{gathered}$$

上述优化问题的解存在两种情况

• 最优值 $=0$，则对应的解满足 $KKT$ 条件
• 最优值 $\neq 0$，则对应的解给出了下降方向，使得多任务目标函数提升（函数值下降）上述优化问题等价于在输入点集凸包中找到最小模点

两个任务的情形

由多目标优化的 $KKT$ 条件，得

$$\begin{gathered} \min _{\alpha^{1}, \ldots \alpha^{T}}\|\gamma \theta+(1-\gamma) \bar{\theta}\| \\ \gamma+(1-\gamma)=1, \gamma \geq 0 \end{gathered}$$

其中 $\theta,\bar{\theta}$ 定义为

$$\begin{aligned} &\theta \triangleq \nabla_{\theta s h} \hat{L}^{1}\left(\theta^{s h}, \theta^{1}\right) \\ &\bar{\theta} \triangleq \nabla_{\theta s h} \hat{L}^{2}\left(\theta^{s h}, \theta^{2}\right) \end{aligned}$$

其解的情况枚举如下

• 当 $\theta^T \bar{\theta} \geq \theta^T \theta,\gamma = 1$
• 当 $\theta^T \bar{\theta} \geq \bar{\theta}^T \bar{\theta},\gamma = 0$
• $\text{otherwise}$

$$\gamma=\frac{(\bar{\theta}-\theta)^{T} \bar{\theta}}{\| \bar{\theta}-\theta) \|_{2}^{2}}p7$$

几何解释

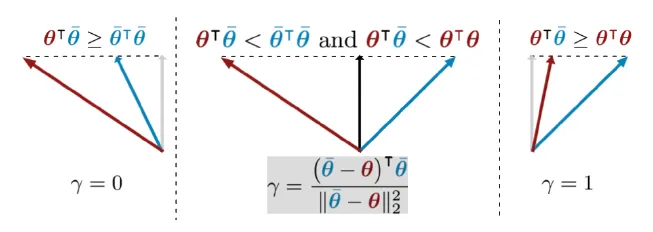
基于 Frank-wolfe 算法，得求解 MTL 任务算法

多任务求解：多个 Pareto 解

上一节介绍的方法只能求得一个 pareto 解，有时需要多个 pareto 解才能做出更好的决策

主要思想

将多任务学习分解为多个带约束的多目标子问题，通过对子问题进行并行求解

原始多任务学习定义

$$\min_{\theta} L(\theta) = (L_1(\theta),L_2(\theta),\cdots,L_i(\theta),\cdots,L_m(\theta))$$

$L_i(\theta)$ 是第 $i$ 个任务的损失函数

下图所示

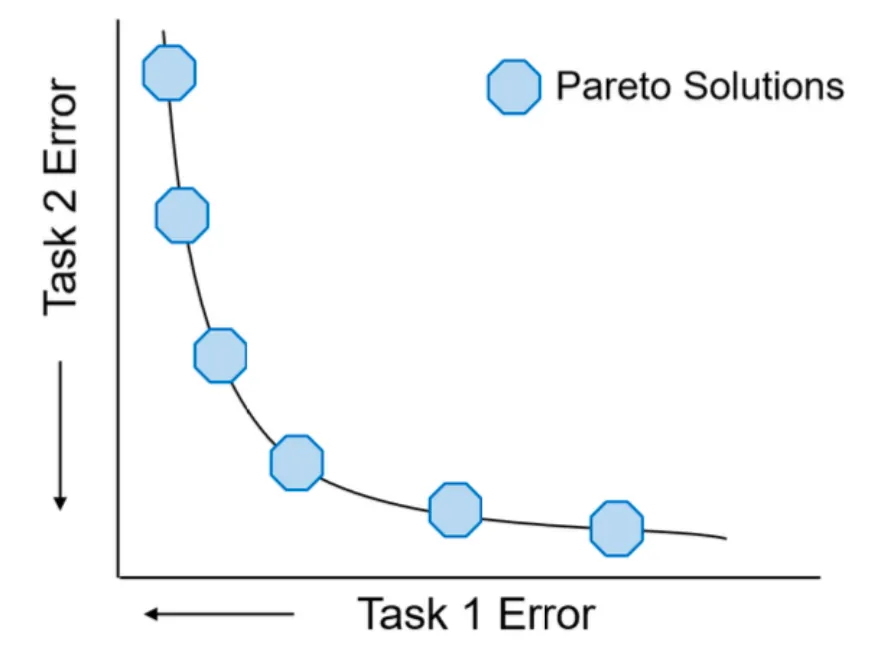
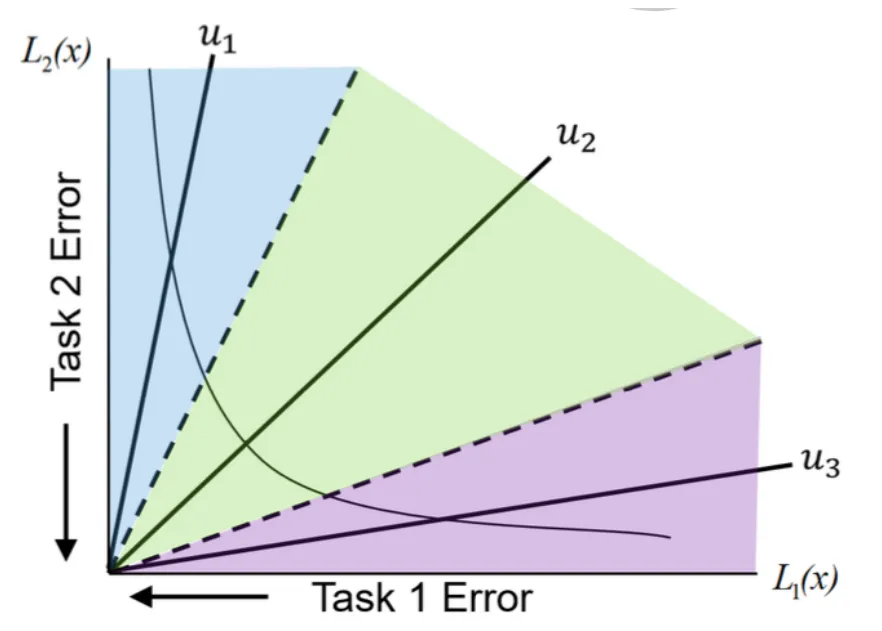
用一组分布良好的 Preference Vectors（PV）将多任务学习的目标空间分解为 $K$ 个子区域

$$PV = \{u_1,u_2,\cdots,u_k,\cdots,u_K\},u_k \in R_+^m$$

重新定义多任务学习

$$\min_{\theta} L(\theta) = (L_1(\theta),L_2(\theta),L_m(\theta)) \\ s.t. \quad L(\theta) \in \Omega_k,k = 1,\cdots,K$$

$\Omega_k$ 是目标空间的子区域

$$\Omega_k = \{v \in R_+^m | u_j^T v \leq u_k^Tv,\forall j = 1,\cdots,K \}$$

$\Omega_k$ 中的元素 $v$

$$v \in \Omega_k \Leftrightarrow u_k^T v = \| u_k \| \cdot \| v \| \cos{\alpha}$$

$u_k^T v$ 为最大的内积

重新定义多任务学习

$$\begin{array}{l} & \min_\theta L(\theta) = (L_1(\theta),L_2(\theta),L_m(\theta)) \\ \text{s.t.} & G_j(\theta_t) = (u_j - u_k)^T \\ & L(\theta_t) \leq 0 \\ & j=1,\cdots,K \end{array}$$

这样得到的解集将会分布在不同的子区域 $\Omega_k$

子问题的梯度下降方法

寻找初始解 $\theta_r$

求解多任务学习，需要找到一个满足约束的基本可行解，对于随机产生的可行解 $\theta_r$ ，一种最直接的方法就是找到初始可行解 $\theta_0$

$$\begin{array}{l} & \min_{\theta_0} \| \theta_0 - \theta_r \|^2 \\ \text{s.t.} & L(\theta_0) \in \Omega_k \end{array}$$

上述问题投影方法求解的效率不高，特别是对于大规模的深度神经网络，改写为无约束优化问题，使用序列梯度方法找到初始解 $\theta_0$

定义活跃限制集合（activated constraints）

$$I(\theta_r) = \{ j|G_j(\theta_r) \geq 0,j=1,\cdots,K \}$$

令 $I(\theta_r)$ 中所有的活跃限制函数值下降的方向

$$(d_r,\alpha_r) = \text{argmin}_{d \in R^n,\alpha \in R} \quad \alpha + \frac{1}{2} \|d\|^2 \\ \text{s.t.} \quad \nabla G_j (\theta_r)^T d \leq \alpha,j\in I(\theta_r)$$

得到更新公式

$$\theta_{r_{t+1}} = \theta_{r_t} + \eta_r d_{r_t}$$

上述方法能将活跃集内的约束目标值减少，使得越来越多的约束目标小于 0，$I(\theta{r})$ 最后变为空集，则 $\theta{r}$ 是可行解

求解子问题

受限 pareto 最优：$\theta^{\ast}$ 是多任务 $L(\theta)$ 在子区域 $\Omega_k$ 的最优解，如果 $\theta^{\ast} \in \Omega_k$ 且不存在 $\hat{\theta} \in \Omega_k$，使得 $\hat{\theta} < \theta^{\ast}$

考虑如下多目标优化问题

$$\begin{array}{l} & (d_t,\alpha_t) = \text{argmin}_{d\in R^n,\alpha \in R} \quad \alpha + \frac{1}{2}\|d\|^2 \\ \text{s.t.} & \nabla L_i(\theta_t)^Td \leq \alpha,i=1,\cdots,m\\ & \nabla G_j(\theta_t)^Td \leq \alpha,j \in I_{\in}(\theta_t) \end{array}$$

其中 $I_{\in}(\theta_t)$ 定义

$$I_{\in} (\theta_t) = \{j \in I | G_j (\theta) \geq - \epsilon \}$$

令 $(d^k,a^k)$ 是多任务学习问题的解，则

• 如果 $\theta_t$ 是严格受限于 $\Omega_k$，则 $d_t = 0 \in R^n$ 且 $\alpha_t = 0$

• 如果 $\theta_t$ 不是严格受限于 $\Omega_k$，则

  $$\begin{array}{l} \alpha_{t} \leq-\frac{1}{2}\left\|d_{t}\right\|^{2}<0 \\ \nabla L_{i}\left(\theta_{t}\right)^{T} d \leq \alpha,& i=1, \ldots, m \\ \nabla G_{j}\left(\theta_{t}\right)^{T} d \leq \alpha,& j \in I_{\epsilon}\left(\theta_{t}\right) \end{array}$$

  迭代公式

  $$\theta_{t+1} = \theta_t + \eta d_t$$

通过求解上述问题，能够获得一个有效的搜索方向

大规模求解方法

上述方法能够获得一个有效的搜索方向，对于大规模的问题，会比较困难，这里将问题重写，将其表示为对偶形式

• $KKT$ 条件

  $$\begin{array}{l} & d_{t} =-\sum_{i=1}^{m} \lambda_{i} \nabla L_{i}\left(\theta_{t}\right)+\sum_{j \in I_{\epsilon}(\theta)} \beta_{i} \nabla G_{j}\left(\theta_{t}\right) \\ \text{s.t.} & \sum_{i=1}^{m} \lambda_{i}+\sum_{j \in I_{\epsilon}(\theta)} \beta_{j}=1 \end{array}$$

• 对偶问题

  $$\begin{array}{l} & \max_{\lambda_{i}, \beta_{j}}-\frac{1}{2}\left\|\sum_{i=1}^{m} \lambda_{i} \nabla L_{i}\left(\theta_{t}\right)+\sum_{j \in I_{\epsilon}(\theta)} \beta_{i} \nabla G_{j}\left(\theta_{t}\right)\right\|^{2} \\ \text { s.t. } & \sum_{i=1}^{m} \lambda_{i}+\sum_{j \in I_{\epsilon}(\theta)} \beta_{j}=1 \\ & \lambda_{i} \geq 0, \beta_{j} \geq 0 \\ & \forall i=1, \cdots, m\\ & \forall j \in I_{\epsilon}(\theta) \end{array}$$

将多任务学习转化为其对偶问题后，求解空间不再是参数空间，而是变成了任务个数和受限条件数，使得求解问题极大的减少了

Pareto MTL 算法如下图

为表述方便，这里引用论文中关于多任务学习的定义

设 $f(x)$ 表面光滑

$$f(x):\mathcal{R}^n \rightarrow \mathcal{R}^m \\ f_i(x):\mathcal{R}^n \rightarrow \mathcal{R},i=1,\cdots,m$$

准备：$Krylov$ 子空间

大规模稀疏线性方程组 $AX=b$ 求解的首先方法是 $krylov$ 子空间方法，基本思想是在一个较小的子空间 $\mathcal{K} \subset R_n$ 中寻找近似解

定义：设 $A \in R^{n \times n},r \in R^n$，则

$$\mathcal{K}_{m}(A, r) \triangleq \text{span}\{r, Ar, \cdots, A^{m-1} r\} \subseteq R_{n}$$

是由 $A$ 和 $r$ 生成的 $Krylov$ 子空间，通常简记为 $\mathcal{K}_m$，$Krylov$ 子空间有如下的三个性质

• $Krylov$ 子空间嵌套性：$\mathcal{K}{1} \subseteq \mathcal{K}{2} \subseteq \cdots \subseteq \mathcal{K}_{m}$
• $\mathcal{K}_m$ 的维数不超过 $m$
• $\mathcal{K}_{m}(A, r)={x=p(A)}$，$r$ 为次数小于 $m$ 的多项式

求解 $Krylov$ 子空间的解来近似原始线性方程组的解

基本概念

• Pareto 平稳点（Pareto Stationary）：设 $f_i(x)$ 连续可身微，点 $x$ 称为 Pareto 平稳点，如果存在 $\alpha \in \mathcal{R}^{m},a_i \geq 0$ 使得下式成立

  $$\sum_{i=1}^{m} \alpha_i \nabla f_i(x) = 0 \\ \sum_{i=1}^{m} \alpha_i = 1$$

• Pareto 点都是 Pareto 平稳点

• 设 $f(x)$ 是光滑且 $x^{\ast}$ 是 Pareto 点，$x(t)$ 是过点 $x^{\ast}$ 的曲线

  $$x(t):t\in (-\epsilon,\epsilon) \rightarrow \mathcal{R}^n \\ x(0) = x^{\ast}$$

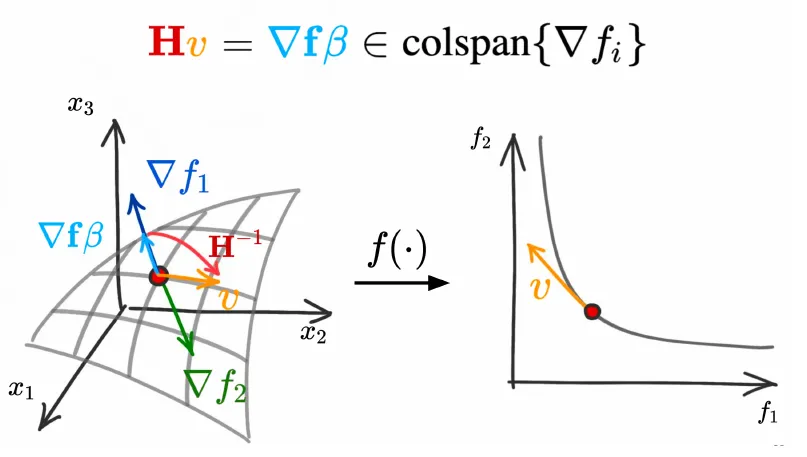
  则存在 $\beta \in \mathcal{R}^m$ 使得

  $$H(x^{\ast})x'(t) = \nabla f(x^{\ast})^T \beta \\ H(x^{\ast}) = \sum_{i=1}^{m} \alpha_i \nabla^2 f_i(x^{\ast})$$

  $x’(t)$ 为切线

上式表明,算子 $H(x^{\ast})$ 将点 $x$ 处的切向量 $v = x’(t)$ 变换为由 $∇f_i(x^{\ast})$ 扩张成的 $Krylov$ 子空间的向量

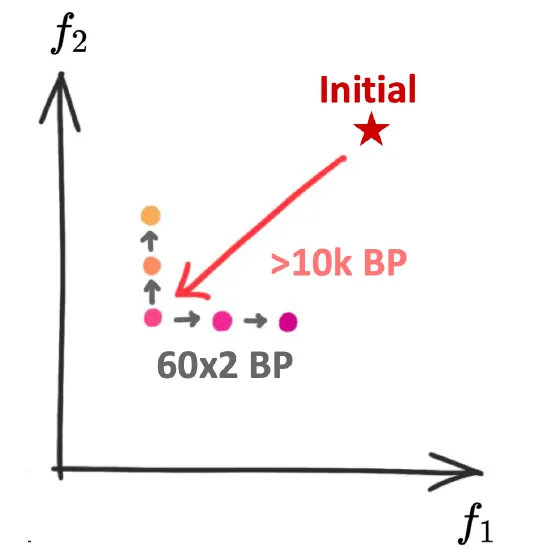
离散 Pareto 求解

给定初始点 $x_0 \in \mathcal{R}^n,f_i(x)$ 光滑，可以从如下三步来获取连续 Pareto 解

• 求解 Pareto 平稳点: 从初始点 $x_0$ 出发，通过梯度下降的方法求解 Pareto 平稳点 $x_0^{\ast}$
• 扩展 Pareto 平稳点，$f(x)$ 在点 $x_0^{\ast}$ 处光滑，如果 Pareto 前沿存在，则在点 $x_0^{\ast}$ 处的某个领域内存在 Pareto 平稳点，由此出发，可以求得一系列的 Pareto 平稳点 $x_i^{\ast}$
• 将已知的平稳点所在的局部 Pareto 前沿进行连接合并，扩充成更大的连续Pareto 前沿

接下来讨论获取 Pareto 平稳点的方法

梯度求解法

见上述

一阶梯度求解法扩张

通过梯度求解法求解出 Pareto 平稳点 $x_0^{\ast}$ 后，基于该点扩展出局部 Pareto 集 ${x_i }$，这一过程分解为两步

• 计算权重 $\alpha$
• 求解搜索方向 $v$，估计梯度迭代的搜索方向 $v_i$

通过如下更新公式求解

$$x_i = x_0^{\ast} + sv_i$$

计算 $\alpha$ 可以归结为求解如下的约束问题

$$\min_\alpha \| \sum_{i=1}^m \alpha_i \nabla f_i(x_0^{\ast}) \|^2 \\ \text{s.t.} \quad \alpha_i \geq 0,\sum_{i=1}^m \alpha_i = 1$$

上述问题规模为 $m$， 量级较小，可以很方便的求解出来

再由基本概念，得求解的线性方程组

$$H(x_0^{\ast})v = \nabla f(x_0^{\ast})^T \beta$$

上述问题求解有两个难点

• $x_0^{\ast}$ 不一定为 Pareto 平稳点
• 当 $n$ 非常大时，求解起来非常困难

为此引入校正向量 $c$（correction vector），约束问题改写为

$$\begin{array}{l} &\min_{a,c} \| c \|^2 \\ \text{s.t.} & \alpha_i \geq 0 \\ & \sum_{i=1}^m \alpha_i = 1 \\ & \sum_{i=1}^{m} \alpha_i(\nabla f_i(x_0^{\ast})-c)=0 \end{array}$$

用 $\nabla f_i(x_0^{\ast})-c$ 近似 $\nabla f_i(x_0^{\ast})$，$x_0^{\ast}$ 将会是 Pareto 平稳点

设 $a^{\ast}$ 是未引入校正向量约束问题的解，则引入 $c$ 后的解为

$$(a,c) = (a^{\ast},\nabla f(x_0^{\ast})^T a^{\ast})$$

在计算出 $a^{\ast},x_0^{\ast},c$ 后，可以计算出 $\nabla f(x_0^{\ast})$，考虑如下稀疏线性方程组

$$H(x_0^{\ast})v = (\nabla f(x_0^{\ast})^T - c^T) \beta$$

$\beta$ 为随机生成的向量，$v$ 为待求解的变量。上述式可以通过 $krylov$ 子空间，$MINERS$ 方法求解

寻找离散 Pareto 解集合的求解算法

• Input：随机初始化网络
• ParetoExpand($x^{\ast}$) 生成点 $x^{\ast}$ 的 $K$ 个搜索方向 $v_i$
• 由 $K$ 个搜索方向扩展出 $K$ 个子网络
• 更新子网络节点 $x_i = x^{\ast} + sv_i$
• ParetoExpand($x_i$) 输出 Pareto 平稳点 $x_i^{\ast}$
• Output：$N$ 个 Pareto 平稳网络

连续 Pareto 解（Pareto front）构建

通过前面求解出来 $N$ 个 Pareto 平稳网络（父节点及 $K$ 个子网络），由离散 Pareto 点合并成更大的连续 Pareto 前沿

给定 $xi^{\ast}$ 及基其对应的 $K$ 个节点 ${ {x_i^{\ast}}_1,\cdots,{x_i^{\ast}}_k }$，定义连续变量 $r{i \rightarrow {i}_j} \in [0,1]$ 以及搜索方向

$$v_{i \rightarrow {i}_j} = {x_i^{\ast}}_j - x_i^{\ast},j = 1,2,\cdots,K$$

$x_i^{\ast}$ 处局部 Pareto 集可以通过下式进行构建

$$S(x_i^{\ast}) = \{x_i^{\ast} + \sum_{i=1}^K r_{i \rightarrow {i}_j} u_{i \rightarrow {i}_j} | r_{i \rightarrow {i}_j} \geq 0,\sum_{i=1}^K r_{i \rightarrow {i}_j} \leq 1 \}$$

$S(x_i^{\ast})$ 是点 $x_i^{\ast}$ 及对应的 $K$ 个子节点 ${ {x_i^{\ast}}_1,\cdots,{x_i^{\ast}}_K }$ 构成的凸包，切平面中切向量的线性组合仍然在切平面

对于 $N$ 个局部 Pareto 集

$$\{ S(x_1^{\ast}),\cdots,S(x_N^{\ast}) \}$$

可以将两两接壤处合并成一个更大的局部 Pareto 集合，全部合并完后，可以生成多个的连续 Pareto 前沿