CUDA编程: PyCUDA编程简介

CUDA 编程

摘要

PyCUDA GPU 编程。主要内容是掌握几种PyCUDA 的基本内核函数，在 Python 中生成和调用并行化的 CUDA C 内核函数，以及了解 PyCUDA 的并行前缀算法。

获取 GPU 信息

首先，需要初始化 CUDA，使用 pycuda.driver.init()或通过import pycuda.autoinit使用autoinit子模块初始化，接下来使用pycuda.driver.Device(i)来访问不同的 GPU 设备，这里笔者的电脑为单 GPU

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import pycuda

import pycuda.driver as drv
drv.init()
# 或
# import pycuda.autoinit
# 进行自动初始化

gpu_device = drv.Device(0)

print('GPU Device Name{}: {}'.format(0, gpu_device.name()))
print('SM Count: {}'.format(gpu_device.MULTIPROCESSOR_COUNT))
print('Shared Memory Size per Thread Block: {} KB'.format(gpu_device.MAX_SHARED_MEMORY_PER_BLOCK / 1024.0))
print('Threads per Thread Block: {}'.format(gpu_device.MAX_THREADS_PER_BLOCK))
print('Threads per SM: {}'.format(gpu_device.MAX_THREADS_PER_MULTIPROCESSOR))
print('Warps per SM: {}'.format(gpu_device.MAX_THREADS_PER_MULTIPROCESSOR / 32))

运行命令

1
python infogpu.py

输出如下，SM 数量为 30，每个线程块的共享内存为 48KB，每个线程块有 1024 个线程，每个 SM 有 1536 个线程，每个 SM 有 48 个线程束

1
2
3
4
5
6
GPU Device Name0: NVIDIA GeForce RTX 3060 Laptop GPU
SM Count: 30
Shared Memory Size per Thread Block: 48.0 KB
Threads per Thread Block: 1024
Threads per SM: 1536
Warps per SM: 48.0

使用 gpuarray 类

PyCUDA 库中，gpuarray 为数据的存储类型，正如 Numpy 库中的 array 为数据的存储类型

传输数据

在 CUDA C 中，我们需要使用 cudaMemcpyHostToDevice和cudaMemcpyDeviceToHost等函数来进行主机与设备的数据传输，需要跟踪主机与设备内存空间中的多个指针，还要进行内存分配，会使代码变得复杂，PyCUDA 的 gpuarray 能够自动完成内存分配，并根据生命周期自动释放。举例如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import pycuda.autoinit
from pycuda import gpuarray
import numpy as np

x_host = np.array([1, 2, 3], dtype=np.float32)
y_host = np.array([4, 5, 6], dtype=np.float32)
z_host = np.array([7, 8, 9], dtype=np.float32)

x_device = gpuarray.to_gpu(x_host)
y_device = gpuarray.to_gpu(y_host)
z_device = gpuarray.to_gpu(z_host)

print((x_device + y_device + z_device).get())
print((x_device ** y_device).get())
print((x_device / z_device).get())

# 输出为
[12. 15. 18.]
[  1.       32.      729.00006]
[0.14285715 0.25       0.33333334]

上面的程序使用gpuarray.to_gpu()将 array 转为 gpuarray，使用 gpuarray 的get()属性将 gpuarray 转为 array，除此之外，gpuarray 还具有如下属性

1
2
3
4
5
6
7
8
9
10
11
12
pycuda.gpuarray.zeros(shape, dtype=np.float64, *, allocator=None, order='C')	# 开辟gpu内存空间，创建 (m,n) 的0矩阵
pycuda.gpuarray.empty(shape, dtype, *, allocator=None, order='C')	# 开辟gpu内存空间，创建 (m,n) 的空矩阵
pycuda.gpuarray.zeros_like(other_ary, dtype=None, order='K')	# 开辟gpu内存空间，创建 size 同 ary 的 0矩阵，因此ary最好
pycuda.gpuarray.empty_like(other_ary, dtype=None, order='K')	# 开辟gpu内存空间，创建 size 同 ary 的空矩阵
pycuda.gpuarray.arange(start, stop, step, dtype=None, stream=None)	# 创建顺序序列
pycuda.gpuarray.take(a, indices, stream=None)	# 返回 gpu_ary[a[index[0]], ..., a[index[n]]]
pycuda.gpuarray.maximum(a, b, out=None, stream=None)	# gpu_ary 对应a和b中的较大元素
pycuda.gpuarray.minimum(a, b, out=None, stream=None)	# gpu_ary 对应a和b中的较小元素
pycuda.gpuarray.max(a, stream=None)	# gpu_ary 所有元素的最大元素
pycuda.gpuarray.min(a, stream=None)	# gpu_ary 所有元素的最小元素
pycuda.gpuarray.sum(a, dtype=None, stream=None)	# gpu_ary 所有元素求和
pycuda.gpuarray.dot(a, b, dtype=None, stream=None)	# gpu_ary 求点积

上述函数中的stream=None意为指定 CUDA 流，我们会在后面的章节详细讲解。

更多属性使用方法请查看官方文档

PyCUDA 生成并行化 Kernel 函数

PyCUDA 提供了大量函数来生成内联的 CUDA C 内核函数，内联函数通过 NVIDIA NVCC 编译器在外部编译缓存，由 PyCUDA 程序在运行时调用，下面为大家举几个主要例子，更详细的 PyCUDA 内核函数介绍请看官方文档

ElementwiseKernel 逐元素运算

ElementwiseKernel函数用于对 gpuarray 数组并行化逐元素计算，函数声明如下

class pycuda.elementwise.ElementwiseKernel(arguments, operation, name='kernel', keep=False, options=[], preamble='')

  • arguments: 意为参数列表，内容是声明变量的字符串，为 C/C++ 语法，末尾无分号
  • operation: 为变量赋值，对数组的操作需要用 i 进行索引，类会自动 并行化 GPU 各核心中与 i 有关的计算，为 C/C++ 语法，末尾无分号
  • name: 指定内核函数名称，命名空间在 CUDA C 中
  • options: 构建时要使用的编译器选项，为list类型
  • keep: 为True则保留编译器输出目录，并打印一行指示其所在目录以用于调试，False则不保留
  • preamble: 指定内核构造之前包含的代码，可以使用它来包含其他文件和定义operation使用的函数

下例的程序定义了一个名为 gpu_x2_kernel的内核函数，实现了输入数组in中每个元素的平方，将结果数组out中

1
2
3
4
5
6
7
8
9
10
11
import numpy as np
import pycuda.autoinit
from pycuda import gpuarray
from time import time
from pycuda.elementwise import ElementwiseKernel
host_data = np.float32(np.random.random(1<<20))
gpu_x2_kernel = ElementwiseKernel(
    "float *in, float *out",    # arguments
    "out[i] = in[i] * in[i]",   # operation
    "gpu_x2_kernel"             # name
)

下面的程序比较了 gpuarray 数组运算与ElementwiseKernel类运算的速度，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import numpy as np
import pycuda.autoinit
from pycuda import gpuarray
from time import time
from pycuda.elementwise import ElementwiseKernel

host_data = np.float32(np.random.random(1<<29))

gpu_x2_kernel = ElementwiseKernel(
    "float *in, float *out",
    "out[i] = in[i] * in[i]",
    "gpu_x2_kernel"
)

def speedcomparison():
    t1 = time()
    host_data_x2 =  host_data * host_data
    t2 = time()
    print("total time to compute on CPU: {}".format(t2 - t1))
    device_data = gpuarray.to_gpu(host_data)
    # allocate memory for output
    device_data_2x = gpuarray.empty_like(device_data)
    t1 = time()
    gpu_x2_kernel(device_data, device_data_2x)
    t2 = time()
    from_device = device_data_2x.get()
    print("total time to compute on GPU: {}".format(t2 - t1))
    print("Is the host computation the same as the GPU computation? : {}".format(np.allclose(from_device, host_data_x2)))

if __name__ == '__main__':
    speedcomparison()
    
# 在 ipython 中运行输出为
In [1]: run speedcomparison.py
total time to compute on CPU: 0.36846113204956055
total time to compute on GPU: 0.07349300384521484
Is the host computation the same as the GPU computation? : True

In [2]: run speedcomparison.py
total time to compute on CPU: 0.368114709854126
total time to compute on GPU: 0.03887605667114258
Is the host computation the same as the GPU computation? : True

In [3]: run speedcomparison.py
total time to compute on CPU: 0.3670005798339844dair_v2x_root
total time to compute on GPU: 0.039081573486328125
Is the host computation the same as the GPU computation? : True

可以看到在首次运行 GPU 的内核函数后，运算时间会大幅减少，这正是因为 NVCC 编译器会编译好的内核函数缓存起来，以重复使用

其中在内核函数中定义的float *out为 C 语言的浮点型指针，所以会使用gpuarray.empty_like先在 GPU 开辟内存空间，将运算结果放入其中，再使用get函数拷贝回主机

InclusiveScanKernel 扫描内核函数

InclusiveScanKernel函数通过指定输入类型dtype和string类型的算术表达式scan_expr进行内核函数构造，再对数组逐元素进行并行化运算，函数声明如下

class pycuda.scan.InclusiveScanKernel(dtype, scan_expr, neutral=None, name_prefix='scan', options=[], preamble='', devices=None)

  • dtype: 指定输入数组类型
  • scan_expr: 任意符合结合律的二元运算表达式，必须是 C 语言编写
  • neutral: 中性元，加法应为 0，乘法应为 1，本小节后面会详细讲解原因
  • name_prefix: 用于内核名称以确保配置文件和日志中的可识别性
  • options 与 preamble 含义同上

下面的程序对向量逐元素作加法以及逐元素查找最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np
import pycuda.autoinit
from pycuda import gpuarray
from pycuda.scan import InclusiveScanKernel

seq1 = np.array(list(range(10)),dtype=np.int32)
seq2 = np.array([1,100,-3,-1000,4,1000000,65,2454],dtype=np.int32)
seq1_gpu = gpuarray.to_gpu(seq1)
seq2_gpu = gpuarray.to_gpu(seq2)
sum_gpu = InclusiveScanKernel(np.int32, "a + b")
max_gpu = InclusiveScanKernel(np.int32, "a>b ? a : b")
print(sum_gpu(seq1_gpu).get())
print(max_gpu(seq2_gpu).get())

# 输出为
[ 0  1  3  6 10 15 21 28 36 45]
[      1     100     100     100     100 1000000 1000000 1000000]

上例所示，sum_gpu为"a + b"，包含a和b代指的二元运算的两个元素，类似 Python 中的 lambda a,b : a + b，max_gpu类似lambda a,b : max(a,b)

ReductionKernel 规约内核函数

ReductionKernel函数对arguments并行执行 map expr，然后对其结果执行 reduce expr，相当于InclusiveScanKernel函数后接着ElementwiseKernel函数，函数声明如下

class pycuda.reduction.ReductionKernel(dtype_out, neutral, reduce_expr, map_expr=None, arguments=None, name='reduce_kernel', keep=False, options=[], preamble='', allocator=None)

  • dtype_out: 指定返回数据类型
  • neutral: 中性元，加法应为 0，乘法应为 1，本小节后面会详细讲解原因
  • reduce_expr: 相当于InclusiveScanKernel函数的reduce_expr
  • map_expr: 相当于ElementwiseKernel函数的operation
  • 其余关键字同上

下面的程序计算了两个向量的点积

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import numpy as np
import pycuda.autoinit
from pycuda import gpuarray
from pycuda.reduction import ReductionKernel

seq1 = np.array(range(10),dtype=np.float32)
seq2 = np.array(range(10),dtype=np.float32)
seq1_gpu = gpuarray.to_gpu(seq1)
seq2_gpu = gpuarray.to_gpu(seq2)
dot_prod = ReductionKernel(np.float32, neutral="0", reduce_expr="a+b", map_expr="x[i] * y[i]",arguments="float *x, float *y")
print(np.dot(seq1,seq2))
print(dot_prod(seq1_gpu, seq2_gpu).get())

# 输出为
285.0
285.0

PyCUDA SourceModule 并行函数

SourceModule函数将原来的内联 CUDA C 代码编译成可以从 Python 启动的内核函数，与上述所有函数不同的是，SourceModule函数在source中直接编写 CUDA C 整体内核函数代码，函数声明如下

class pycuda.compiler.SourceModule(source, nvcc='nvcc', options=None, keep=False, no_extern_c=False, arch=None, code=None, cache_dir=None, include_dirs=[])

  • source: 内核函数代码，使用 CUDA C 编写
  • nvcc: 编译器命令
  • no_extern_c: 默认为 False，source会被包装在 extern “C” { … } 中以防止 C++ 名称重整，为True则不会被包装在 extern “C” { … } 中
  • arch: 指定传递给 nvcc 命令上 -arch 选项的值
  • code: 指定传递给 nvcc 命令上 -code 选项的值
  • cache_dir: 指定用于编译器缓存的目录，默认为PYCUDA_CACHE_DIR所指目录，为False则禁用缓存，如果环境变量PYCUDA_DISABLE_CACHE被赋值，意为全局禁用缓存，cache_dir将被覆盖
  • include_dirs: 将一个或多个外部类传递给source，类型为 string list
  • 其余关键字同上

需要使用get_function得到已编译好的内核函数的引用，才可使用内核函数，下例程序计算了矩阵乘法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
import pycuda.driver as cuda
import pycuda.tools
import pycuda.autoinit
import numpy as np
import numpy.linalg as la
from pycuda import gpuarray
from pycuda.compiler import SourceModule
import time
 
mod = SourceModule("""
__global__ void matrixMultiply(float * A, float * B, float * C,
                   int A_shape_0,int A_shape_1,int B_shape_1) {
    float cValue = 0;
    int Row = blockIdx.y * blockDim.y + threadIdx.y;
    int Col = blockIdx.x * blockDim.x + threadIdx.x;
    if ((Row < A_shape_0) && (Col < B_shape_1)) {
        for (int k = 0; k < A_shape_1; k++) {
            cValue += A[Row*A_shape_1 + k] * B[k*B_shape_1 + Col];
        }
        C[Row*B_shape_1 + Col] = cValue;
    }
}
""")
 
matrixMultiply = mod.get_function("matrixMultiply")
n = 1000
A = np.random.randint(0,10,1000000).reshape(1000,1000).astype(np.float32)
B = np.random.randint(0,10,1000000).reshape(1000,1000).astype(np.float32)

BLOCK_SIZE = 32

A_gpu = gpuarray.to_gpu(A)
B_gpu = gpuarray.to_gpu(B)
C_gpu = gpuarray.empty_like(A_gpu)

if n % BLOCK_SIZE != 0:
    grid=(n // BLOCK_SIZE+1, n // BLOCK_SIZE+1,1)
else:
    grid=(n // BLOCK_SIZE, n // BLOCK_SIZE,1)

print("grid size: {}".format(grid))
start = time.time()
matrixMultiply(A_gpu, B_gpu, C_gpu, np.int32(A.shape[0]),np.int32(A.shape[1]),np.int32(B.shape[1]), block=(BLOCK_SIZE,BLOCK_SIZE,1), grid=grid);

print("result:\n", C_gpu.get())
print("time cost: %ss" %(time.time() - start))

# 输出为
grid size: (32, 32, 1)
result:
 [[19305. 18274. 18786. ... 19130. 19501. 18229.]
 [19945. 19823. 20158. ... 19853. 20397. 19848.]
 [20651. 19959. 20910. ... 20715. 21033. 20364.]
 ...
 [20196. 19777. 20198. ... 20291. 20736. 19916.]
 [20239. 19820. 20210. ... 20171. 20685. 19244.]
 [19595. 19444. 19546. ... 19862. 20462. 19508.]]
time cost: 0.003673076629638672s

并行前缀算法

前面提到的InclusiveScanKernel函数和函数就是并行扫描算法之一，并行扫描算法定义如下

定义二元运算符 $\oplus$ 和一个有 $n$ 个元素的数组 $[x0, x_1, x_2, \cdots, x{n-1}]$

返回

以加法举例，输入为 [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]，返回为[ 0 1 3 6 10 15 21 28 36 45]，如果用串行的计算方式，需要计算 $n$ 次求和，时间复杂度为$O(n)$，我们要尽量降低时间复杂度

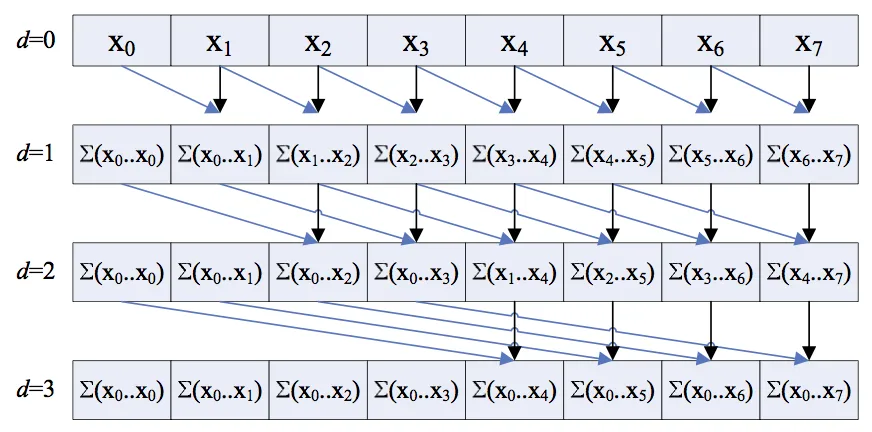
朴素并行前缀算法

朴素并行扫描算法是并行扫描算法的初始版本，我们假设输入元素为 n 个，且 n 为 2 的次幂，同时在 n 个线程上并行计算，时间复杂度为 $O(\log_{2} n)$，下图为算法示意图（原图链接）

下面的程序以加法为例，计算了长度为 1024 的数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import pycuda.autoinit
import pycuda.driver as drv
import numpy as np
from pycuda import gpuarray
from pycuda.compiler import SourceModule
from time import time

naive_ker = SourceModule("""
__global__ void naive_scan(double *vec, double *out) {
     __shared__ double sum_buf[1024];     
     int tid = threadIdx.x;
     sum_buf[tid] = vec[tid];
     
     // begin parallel prefix sum algorithm
     
     int iter = 1;
     for (int i=0; i < 10; i++) {
         __syncthreads();
         if (tid >= iter ) {
             sum_buf[tid] = sum_buf[tid] + sum_buf[tid - iter];
         }
         iter *= 2;
     }
    __syncthreads();
    out[tid] = sum_buf[tid];
    __syncthreads();
}
""")

naive_gpu = naive_ker.get_function("naive_scan")

testvec = np.random.randn(1024).astype(np.float64)
testvec_gpu = gpuarray.to_gpu(testvec)
    
outvec_gpu = gpuarray.empty_like(testvec_gpu)
naive_gpu( testvec_gpu , outvec_gpu, block=(1024,1,1), grid=(1,1,1))

total_sum = sum( testvec)
total_sum_gpu = outvec_gpu[-1].get()

print("Does our kernel work correctly? : {}".format(np.allclose(total_sum_gpu , total_sum)))

其中使用了__syncthreads()函数，保证了线程块中的所有线程在进入下一次迭代前，当前迭代里每一个线程的所有部分都被保存在了全局内存中

高效并行前缀算法

上一例的算法只能计算长度为 1024 的数组进行计算，且需要与长度等量的线程数量，接下来我们实现支持长度超过 1024 的任意数组的算法，此算法需要两个内核函数和 python 函数，分加进行上行扫描和下行扫描。上行扫描阶段类似于一次规约操作，即$x0 \oplus \cdots \oplus x{n-1}$，下行扫描阶段将对上行扫描的返回值进行计算，返回最终结果，具体代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
from __future__ import division
import pycuda.autoinit
import pycuda.driver as drv
import numpy as np
from pycuda import gpuarray
from pycuda.compiler import SourceModule
from time import time

# this is a work-efficent parallel prefix-sum algorithm.
# written by Brian Tuomanen for "Hands On GPU Programming with Python and CUDA"

# kernel for up-sweep phase
up_ker = SourceModule("""
__global__ void up_ker(double *x, double *x_old, int k ) {
     int tid =  blockIdx.x*blockDim.x + threadIdx.x;
     
     int _2k = 1 << k;
     int _2k1 = 1 << (k+1);
     
     int j = tid* _2k1;
     
     x[j + _2k1 - 1] = x_old[j + _2k -1 ] + x_old[j + _2k1 - 1];
}
""")

up_gpu = up_ker.get_function("up_ker")

# implementation of up-sweep phase
def up_sweep(x):
    # let's typecast to be safe.
    x = np.float64(x)
    x_gpu = gpuarray.to_gpu(np.float64(x) )
    x_old_gpu = x_gpu.copy()
    for k in range( int(np.log2(x.size) ) ) : 
        num_threads = int(np.ceil( x.size / 2**(k+1)))
        grid_size = int(np.ceil(num_threads / 32))
        
        if grid_size > 1:
            block_size = 32
        else:
            block_size = num_threads
            
        up_gpu(x_gpu, x_old_gpu, np.int32(k)  , block=(block_size,1,1), grid=(grid_size,1,1))
        x_old_gpu[:] = x_gpu[:]
        
    x_out = x_gpu.get()
    return(x_out)

# kernel for down-sweep phase
down_ker = SourceModule("""
__global__ void down_ker(double *y, double *y_old,  int k) {
     int tid =  blockIdx.x*blockDim.x + threadIdx.x;
     
     int _2k = 1 << k;
     int _2k1 = 1 << (k+1);
     
     int j = tid*_2k1;
     
     y[j + _2k - 1 ] = y_old[j + _2k1 - 1];
     y[j + _2k1 - 1] = y_old[j + _2k1 - 1] + y_old[j + _2k - 1];
}
""")

down_gpu = down_ker.get_function("down_ker")

# implementation of down-sweep phase
def down_sweep(y):
    y = np.float64(y)
    y[-1] = 0
    y_gpu = gpuarray.to_gpu(y)
    y_old_gpu = y_gpu.copy()
    for k in reversed(range(int(np.log2(y.size)))):
        num_threads = int(np.ceil( y.size / 2**(k+1)))
        grid_size = int(np.ceil(num_threads / 32))
        if grid_size > 1:
            block_size = 32
        else:
            block_size = num_threads
        down_gpu(y_gpu, y_old_gpu, np.int32(k), block=(block_size,1,1), grid=(grid_size,1,1))
        y_old_gpu[:] = y_gpu[:]
    y_out = y_gpu.get()
    return(y_out)

# full implementation of work-efficient parallel prefix sum
def efficient_prefix(x):
	return(down_sweep(up_sweep(x)))

testvec = np.random.randn(32*1024).astype(np.float64)
testvec_gpu = gpuarray.to_gpu(testvec)

outvec_gpu = gpuarray.empty_like(testvec_gpu)

prefix_sum = np.roll(np.cumsum(testvec), 1)
prefix_sum[0] = 0

prefix_sum_gpu = efficient_prefix(testvec)
print("Does our work-efficient prefix work? {}".format(np.allclose(prefix_sum_gpu, prefix_sum)))
- ETX   Thank you for reading -
  • Copyright: All posts on this blog except otherwise stated, All adopt CC BY-NC-ND 4.0 license agreement. Please indicate the source of reprint!